Các bạn hãy lưu lại những kiến thức Toán lớp 6 trong bài viết này để vận dụng làm bài tập. Trong Phần 1 này, cùng thầy cô tổng hợp kiến thức của Chương I (Ôn tập và Bổ túc về số tự nhiên) sẽ giúp các bạn có nền tảng vững hơn nhé.
Tập hợp. Phần tử của tập hợp:
- Tập hợp là một khái niệm cơ bản. Tên tập hợp được đặt bằng chữu cái in hoa
- Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu “;” (nếu có phần tử số) hoặc dấu “,”. Mỗi phần tử được liệt kê một lần.
- Một tập hợp có thể có một phần tử, nhiều phần tử, vô số phần tử hoặc cũng có thể không có phần tử nào (tập hợp rỗng).
- Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.
- Quy ước: Tập hợp rỗng là tập hợp con của mọi tập hợp.
Tập hợp các số tự nhiên N
- Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Điểm biểu diễn số tự nhiên a trên tia số gọi là điểm a.
- Tập hợp các số tự nhiên khác 0 được kí hiệu là N*
- Thứ tự:
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia. Trên hai điểm trên tia số, điểm ở bên trái biểu diễn số nhỏ hơn.
+ Nếu a<b và b<c thì a<c.
+ Mỗi số tự nhiên có một số liền sau duy nhất, chẳng hạn số tự nhiên liền sau số 2 là số 3; số liền trước số 3 là số 2; số 2 và số 3 là hai số tự nhiên liên tiếp. Hai số tự nhiên liên tiếp thì hơn kém nhau một đơn vị.
+ Số 0 là số tự nhiên nhỏ nhất. Không có số tự nhiên lớn nhất
+ Tập hợp các số tự nhiên có vô số phần tử
Các phép toán
a. Phép cộng:
a + b = c
(số hạng) + (số hạng) = (tổng)
b. Phép trừ:
Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao cho b + x =a thì ta có phép trừ:
a – b = x
(số bị trừ) – (số trừ) = (hiệu)
c. Phép nhân:
a . b = d
(thừa số) . (thừa số) = (tích)
d. Phép chia:
Cho hai số tự nhiên a và b, trong đó b khác 0. Nếu có số tự nhiên x sao cho b . x = a thì ta nói a chia hết cho b và ta có phép chia hết
a : b = x
(số bị chia) : (số chia) = (thương)

- Tính chất của phép cộng và phép nhân số tự nhiên:

Tính chất giao hoán:
+ Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
+ Khi đổi chỗ các thừa số trong một tích thì tích không đổi.
Tính chất kết hợp:
+ Muốn cộng một tổng hai số với một số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
+ Muốn nhân một tích hai số với một số thứ ba, ta có thể nhân số thứ nhất với tích của số thứ hai và số thứ ba
Tính chất phân phối của phép nhân đối với phép công:
Muốn nhân một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng, rồi cộng các kết quả lại.
e. Cần nhớ
+ Có thể thực hiện tương tự với tính chất a(b – c) = ab – ac

f. Phép nâng lên lũy thừa:

- Nhân hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: am . an = am+n
- Chia hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ các số mũ: am : an = am – n (với a khác 0; m lớn hơn hoặc bằng n)
- Ngoài ra: (am )n = am.n ; (a.b)n = an . bn
- Số chính phương: là số bằng bình phương của một số tự nhiên (ví dụ: 0, 1, 4, 9,…)
Thứ tự thực hiện các phép tính:

Tính chất chia hết của một tổng:

Dấu hiệu chia hết cho 2, 3, 5, 9:
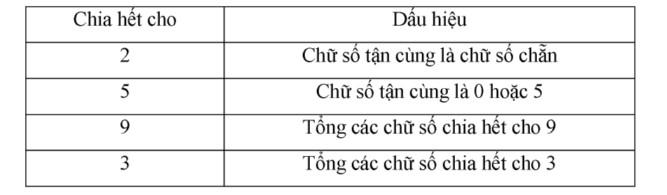
Ước và bội:
- Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.
- Có thể tìm các bội của một số bằng cách nhân số đó lần lượt với 0, 1, 2, 3,…
- Có thể tìm các ước của a bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.
- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó. Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.
Cách kiểm tra 1 số là số nguyên tố:
Để kết luận số a là số nguyên tố (a>1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.
- Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Cách tính số lượng các ước của một số m (m>1):
Xét dạng phân tích của số m ra thừa số nguyên tố:
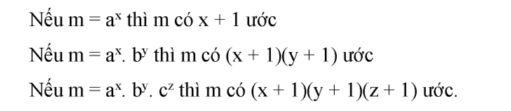
- Ước chung của hai hay nhiều số là ước của tất cả các số đó.
- Bội chung của hai hay nhiều số là bội của tất cả các số đó
- ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
- Các số nguyên tố cùng nhau là các số có ƯCLN bằng 1
- BCNN của hai hay nhiều số là số lớn nhất khác 0 trong tập hợp các bội chung của các số đó.
- Để tìm BC của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.
Cách tìm ƯCLN và BCNN:
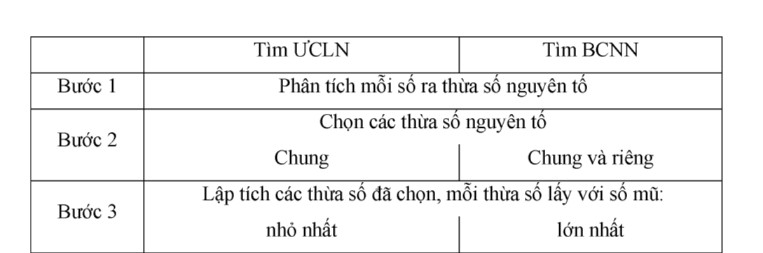
Lưu ý:
+ Tích của hai số tự nhiên khác 0 bằng tích của ƯCLN và BCNN:
a . b = ƯCLN (a,b) . BCNN (a, b)
+ Nếu tích a.b chia hết cho m, trong đó b và m là hai số nguyên tố cùng nhau thì a chia hết cho m
+ Một cách khác tìm ƯCLN của hai số a và b (với a>b): Chia số lớn cho số nhỏ.
Nếu a chia hết cho b thì ƯCLN(a,b) = b
- Nếu phép chia a cho b có số dư r1, lấy b chia cho r1.
- Nếu phép chia b cho r1 có số dư r2, lấy r1 chia cho r2.
- Chia cho đến khi số dư bằng 0 thì số chia cuối cùng là ƯCLN phải tìm.


